Speeding up the Quantum Adiabatic Algorithm
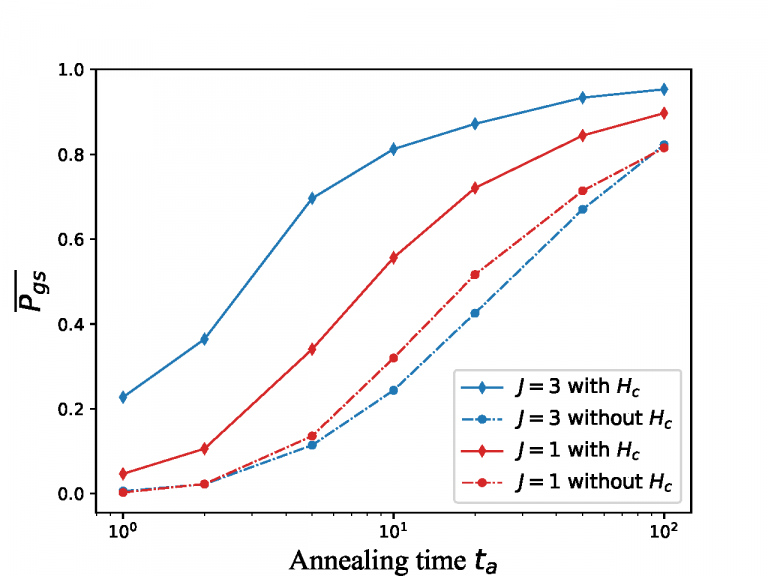
One of the great expectations for quantum computers is that they will be able to solve optimization problems faster than classical computers. The first algorithm to show real promise in this regard was the quantum adiabatic algorithm. In this algorithm, a very simple state of the quantum computer is slowly transformed into a state that encodes the solution of the problem. Speed is everything – that’s why we want to have quantum computers in the first place. In the figure shown here, the approach to the exact solution at 1.0 on the vertical axis is shown as a function of time for the original QAA (dashed lines), and for our version (solid lines). The substantial speedup is achieved by modifying the evolution of the quantum state so that it does not localize in small parts of the state space that are disconnected from one another.
Discrete Scale Invariance in Topological Materials
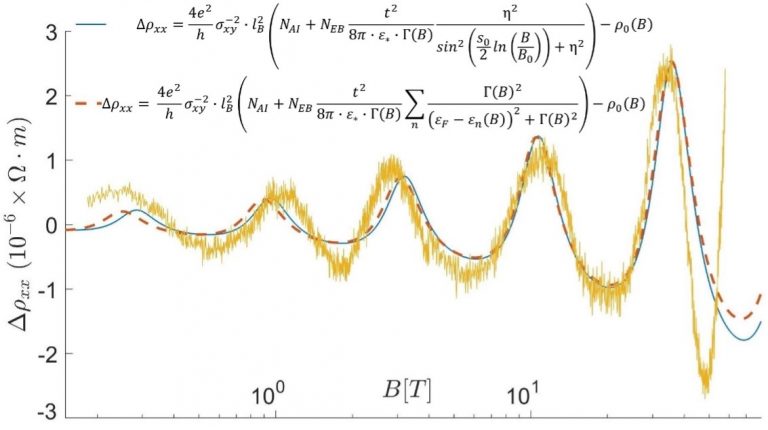
Shown here is the resistivity ρ of ZrTe5, a Weyl semimetal as a function of magnetic field B. ρ(B) is periodic in log B. This is the first time that oscillations with this kind of periodicity have ever been seen in a condensed-matter system. We explained these oscillations by pointing out that the scattering Hamiltonian of Coulomb impurities has discrete scale invariance. This kind of symmetry is very rare in physics. It turns out that the application of a magnetic field is required to bring out this remarkable property.
Evanescent-wave Johnson Noise Producing Qubit Decoherence
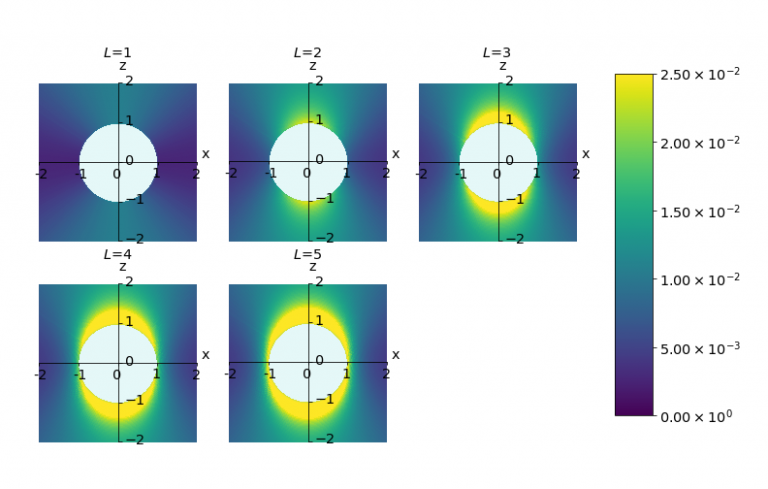
The free electrons in metals move randomly, producing noisy electromagnetic fields in their vicinity. These fields can decohere qubits, so metallic elements in qubit devices can degrade the performance of the device. We have developed the theory of these fields over a number of years. The figure presents the first results for the correlations of the horizontal component of the magnetic field near a metallic sphere as the number of multipole components is increased.
Determining the Sources of Noise that Degrade Spin Qubit Operation
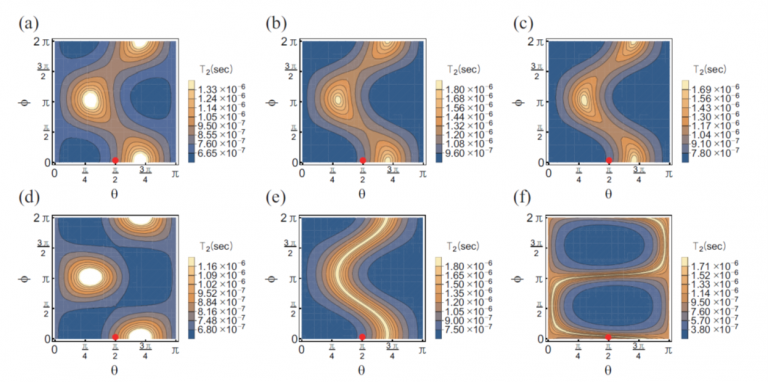
Environmental noise impedes coherent operations of spin qubits by limiting the qubit relaxation (T1) and dephasing (Tφ) times. There are multiple sources of such noise, which makes it important to devise experimental techniques that can detect the spatial locations of these sources and determine which is the most important. We propose that anisotropy in T1 and Tφ with respect to the direction of the applied magnetic field can reveal much about these aspects of the noises.
With PhD student Yujun Choi
Speeding up the Quantum Approximate Optimization Algorithm
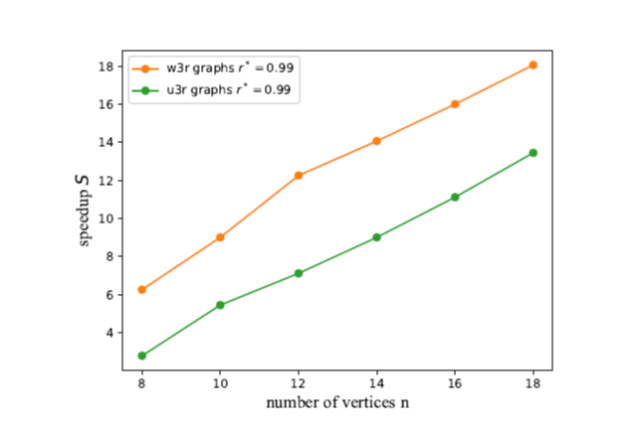
The quantum approximate optimization algorithm transforms a simple many-qubit wavefunction into one which encodes the solution to a difficult classical optimization problem. We modify this procedure by updating the operators themselves to include local fields, using information from the measured wavefunction at the end of one iteration step to improve the operators at later steps. It is shown by numerical simulation on MAXCUT problems that this decreases the runtime of QAOA substantially. This improvement appears to increase with the problem size.
With MS student Carter Dewey and others.